Please read posts on MDP and Bellman Equations prior this post.

Bellman Equations for Optimal Value Functions

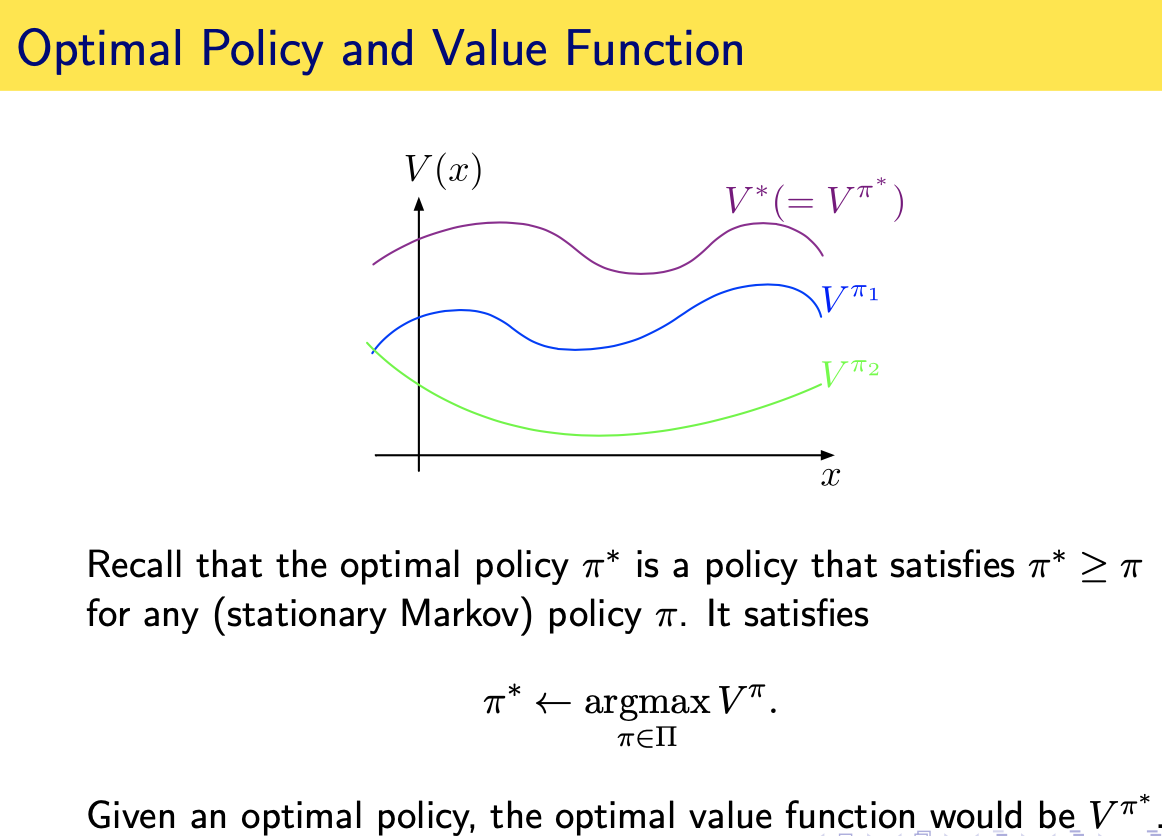
So it is natural to ask, does the optimal value function of optimal policy \(V^{\pi^*}\) have similar recursive structure? the answer is yes, however, we need to prove this. The proof goes with 3 claims which we will prove later:

1. 1. \(\exists\) a value function \(V^*\) s.t \(\forall x \in X\), we have:

      \[V^{*}(x) = max_{a} \{Q^{*}(x, a)\} = max_{a} \{r(x, a) + \gamma \int P(dx^\prime | x, a) V^{*}(x^\prime)\}\]

   2. \(\exists\) a value function \(Q^*\) s.t \(\forall x, a \in X, A\), we have:

      \[Q^{*}(x, a) = r(x, a) + \gamma \int P(dx^\prime | x, a) max_{a^\prime} \{Q^{*} (x^\prime, a^\prime)\}\]

   These equations are called bellman optimality equations for the value functions

2. \(V^{*}\) is the same as \(V^{\pi^*}\), the optimal value function when \(\pi\) is restricted to be within the space of all stationary and non-stationary policies.

3. For discounted continuing MDPs, we can always find a stationary policy that is optimal within the space of all stationary and non-stationary policies.

In summary, we claim that:

\(V^{*}\) exists and it is unique, \(V^{*} = V^{\pi^{*}}\). Same for \(Q^{*}\)

Bellman Operators

In order to prove the claims, we need several concepts:

These operators are linear and recall that:

\[Q^{\pi} (x, a) = r(x, a) + \gamma \int P(dx^\prime | x, a) V^{\pi}(x^\prime) = r(x, a) + \gamma \int P(dx^\prime | x, a) \pi (a^\prime | x^\prime) Q^{\pi} (x^\prime, a^\prime)\]

This implies \(T^{\pi} Q^{\pi} = Q^{\pi}\), same for state-value function and bellman optimality operators. Thus, we can conclude that:

\[V^{\pi} = T^{\pi} V^{\pi}\] \[Q^{\pi} = T^{\pi} Q^{\pi}\] \[V^{*} = T^{*} V^{*}\] \[Q^{*} = T^{*} Q^{*}\]

Properties of Bellman Operators

Bellman operators have several important properties. The properties that matters for us the most are:

1. Monotonicity
2. Contraction

Monotonicity

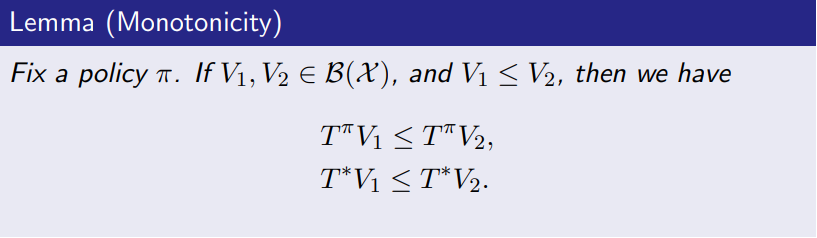
we can easily prove this (only prove \(T^{\pi}\), \(T^{*}\) is the same):

Assume:

\[V_1(x^{\prime}) \geq V_2(x^{\prime}), \forall x^{\prime} \in X\]

we get that for any \(x \in X\):

\[T^{\pi}V_{1} (x) = r^{\pi} (x) + \gamma \int P^{\pi}(dx^{\prime} | x) V_{1} (x^\prime) \geq r^{\pi} (x) + \gamma \int P^{\pi}(dx^{\prime} | x) V_{2} (x^\prime) = T^{\pi}V_2(x)\]

Thus:

\[T^{\pi}V_{1} (x) \geq T^{\pi}V_{2} (x)\]

Contraction

we can also easily prove that \(T^{*}, T^{\pi}\) are contraction mappings (only prove \(T^{\pi}\), \(T^{*}\) is the same):

Consider two action-value functions:

\[Q_1, Q_2 \in B(X\times A)\]

Consider the metric:

\[d(Q_1, Q_2) = \| Q_1 - Q_2 \|_{\infty}\]

We show the contraction w.r.t \(l-\infty\) norm.

For any \((x, a) \in X \times A\), we have:

\[\begin{aligned} \lvert T^{\pi} Q_1 (x, a) - T^{\pi} Q_2 (x, a) \rvert &= \lvert r (x, a) + \gamma \int P(dx^{\prime} | x, a) \pi(da^\prime | x^\prime) Q_{1} (x^\prime, a^{\prime}) - r (x, a) - \gamma \int P(dx^{\prime} | x, a) \pi(da^\prime | x^\prime) Q_{2} (x^\prime, a^{\prime}) \rvert\\ & = \gamma \lvert \int P(dx^{\prime} | x, a) \pi(da^\prime | x^\prime) [Q_{1} (x^\prime, a^{\prime}) - Q_{2} (x^\prime, a^{\prime})] \rvert\\ & \leq \gamma \int \underbrace{P(dx^{\prime} | x, a) \pi(da^\prime | x^\prime)}_{\text{these are probabilities which $ \geq $ 0}} \lvert [Q_{1} (x^\prime, a^{\prime}) - Q_{2} (x^\prime, a^{\prime})] \rvert\\ & \leq \gamma \int P(dx^{\prime} | x, a) \pi(da^\prime | x^\prime) \sup_{x, a}\lvert [Q_{1} (x, a) - Q_{2} (x, a)] \rvert\\ & = \gamma \sup_{x, a}\lvert Q_{1} (x, a) - Q_{2} (x, a) \rvert \underbrace{\int P(dx^{\prime} | x, a) \pi(da^\prime | x^\prime)}_{\text{this is a probability distribution which sums to 1}}\\ & = \gamma \sup_{x, a}\lvert Q_{1} (x, a) - Q_{2} (x, a) \rvert = \gamma \|Q_{1} - Q_{2}\|_{\infty} \end{aligned}\]

This inequality holds for all state action pair, thus, we have showed that bellman operators are contraction mappings.

Consequences of Monotonicity and Contraction

Uniqueness of fixed points

Proof of the proposition is also simple (Same for \(Q^{\pi}, Q^{*}\)):

For any \(\pi\), \(T^{\pi}\) is a \(\gamma-\)contraction mapping (same for \(T^{*}\)), thus, by the Banach fixed point theorem, they have unique fixed point

\[T^{*} V^{*} = V^{*}, T^{\pi} V^{\pi} = V^{\pi}\]

Moreover, the update rule \(V_{k+1} \leftarrow T^{\pi} V_{k}\) converges, which means:

\[lim_{k \rightarrow \infty} \| V_{k} - V^{\pi}\|_{\infty} = 0\]

Value of the greedy policy of \(V^{*}\) is \(V^{*}\)

We know if:

\[T^{\pi} V^{*} = T^{*}V^{*} \implies T^{\pi} V^{*} = V^{*}\]

This is also the fix point of \(T^{\pi}\), this implies \(V^{\pi} = V^{*}\).

On the other hand, if we know \(V^\pi = V^{*}\), the by applying \(T^{\pi}\) to both side we have

\[T^{\pi} V^{\pi} = T^{\pi} V^{*} \implies T^{\pi} V^{\pi} = T^{*} V^{*} = T^{\pi} V^{*}\]

Thus, we can conclude that:

\[T^{\pi} V^{*} = T^{*}V^{*} \text{ iff } V^\pi = V^{*}\]

The Connection To Greedy Policy

Given \(V^{*}\), the greedy policy of \(V^{*}\) is defined as:

\[\pi_{g} (x; V^{*}) = argmax_{a \in A} Q^{*}(x, a) = argmax_{a \in A} r(x, a) + \gamma \int P(dx^{\prime} | x, a) V^{*}(x^{\prime})\]

So:

\[T^{\pi_{g} (x; V^{*})} V^{*} = r(x, \pi_{g} (x; V^{*})) + \gamma \int P(dx^{\prime} | x, \pi_{g} (x; V^{*})) V^{*}(x^{\prime}) = max_{a \in A} r(x, a) + \gamma \int P(dx^{\prime} | x, a) V^{*}(x^{\prime})\]

Compare with \(T^{*} V^{*}\):

\[T^{*} V^{*} = max_{a \in A} r(x, a) + \gamma \int P(dx^{\prime} | x, a) V^{*}(x^{\prime})\]

Thus:

\[T^{*} V^{*} = T^{\pi_{g} (x; V^{*})} V^{*}\]

Since:

\[T^{\pi} V^{*} = T^{*}V^{*} \text{ iff } V^\pi = V^{*} \implies V^{*} = V^{\pi_{g} (x; V^{*})}\]

That is, the value of following \(\pi_{g} (x; V^{*})\) is the same as \(V^{*}\). This means that if we find \(V^{*}\) and its greedy policy, the value of following the greedy policy is \(V^{*}\).

To find an optimal policy, we can find \(V^{*}\) first, then find its greedy policy

following this conclusion: Although we have not yet prove that \(V^{*}\) is the optimal value function (\(\pi^{*} = argmax_{\pi \in \prod} V^{\pi} (x)\), \(V^{*} = V^{\pi^{*}}\) (claim 2)), this is indeed true. (prove later)

An error bound based on the bellman error

If we find a V s.t \(V = T^{*} V\), we know that \(V = V^{*}\) (same for \(T^{\pi} and Q\)), what if \(V \approx T^{*} V\), what can we say about the closeness of \(V\) to \(V^{*}\)?

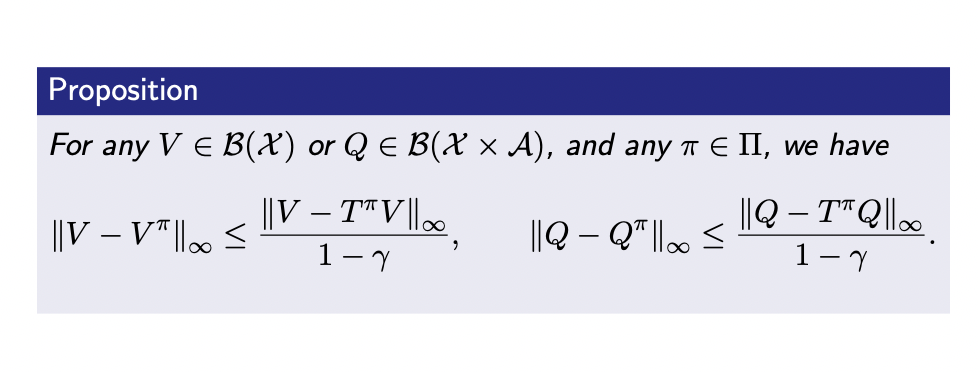
Proof:

\[\begin{aligned} V - V^{*} &= V - T^{*} V + T^{*} V - V^{*}\\ \implies \| V - V^{*} \|_{\infty} &= \| V - T^{*} V + T^{*} V - V^{*} \|_{\infty}\\ &\leq \|V - T^{*} V \|_{\infty} + \|T^{*} V - T^{*}V^{*} \|_{\infty} \\ &\leq \|V - T^{*} V \|_{\infty} + \gamma \|V - V^{*} \|_{\infty} (i.e. \|T^{*} V - T^{*}V^{*} \|_{\infty} \leq \gamma \|V - V^{*} \|_{\infty}, \text{contraction property} )\\ \implies \| V - V^{*} \|_{\infty} &\leq \frac{\|V - T^{*} V \|_{\infty}}{(1 - \gamma)}\\ \implies \| V - V^{*} \|_{\infty} &\leq \frac{BE^{*}}{(1 - \gamma)} \end{aligned}\]

Proof of claim 2: \(V^{*} = T^{*} V^{*}\) is the same as \(V^{\pi^{*}}\)

The proof has three parts:

1. Prove that \(V^{*} (x) \leq sup_{\pi \in \prod} V^{\pi} (x)\)

2. Prove that \(V^{*} (x) \geq sup_{\pi \in \prod} V^{\pi} (x)\)

3. Combine 1 and 2, we show that claim 2 is true, that is, \(V^{*} = T^{*} V^{*}\) is the same as \(V^{\pi^{*}}\)

Proof \(V^{*} (x) \leq sup_{\pi \in \prod} V^{\pi} (x)\)

From the error bound with the choice of \(V = V^{*}\), we have for any \(\pi \in \prod\),

\[\| V^{*} - V^{\pi} \|_{\infty} \leq \frac{\| V^{*} - T^{\pi}V^{*} \|_{\infty}}{1 - \gamma}\]

Let \(\epsilon > 0\). Choose a policy \(\pi_{\epsilon}\) s.t:

\[\| V^{*} - T^{\pi_{\epsilon}} V^{*} \|_{\infty} \leq (1 - \gamma) \epsilon\]

We know that this \(\pi_{\epsilon}\) exists because we can always pick a \(\pi_{\epsilon}\) s.t it is the maximizer of \(T^{*}V^{*}\) (ie. pick \(\pi_{\epsilon}\) to be \(\pi_{g} (x; V^{*})\), from above proof we know that \(T^{\pi_{g} (x; V^{*})} V^{*} = T^{*} V^{*}\)), then:

\[\| V^{*} - T^{\pi_{\epsilon}} V^{*} \|_{\infty} = 0 \leq (1 - \gamma) * \epsilon, \forall \epsilon > 0\]

For any policy \(\pi_{\epsilon}\) that satisfies above equation:

\[\| V^{*} - V^{\pi_{\epsilon}} \|_{\infty} \leq \epsilon\]

This means that:

\[sup_{x_i} \{|V^{*} (x_i) - V^{\pi_{\epsilon}} (x_i)|\} \leq \epsilon\]

\[\implies |V^{*} (x_i) - V^{\pi_{\epsilon}} (x_i)| \leq sup_{x_i} \{|V^{*} (x_i) - V^{\pi_{\epsilon}} (x_i)|\} \leq \epsilon, \forall x_i \in X\]

\[\implies V^{*} (x_i) - V^{\pi_{\epsilon}} (x_i) \leq |V^{*} (x_i) - V^{\pi_{\epsilon}} (x_i)| \leq \epsilon\]

\[\implies V^{*} (x_i) \leq \epsilon + V^{\pi_{\epsilon}} (x_i)\]

Since:

\[V^{\pi_{\epsilon}} (x) \leq sup_{\pi \in \prod} V^{\pi} (x)\]

As we take \(\epsilon \rightarrow 0\), we have:

\[V^{*} (x) \leq lim_{\epsilon \rightarrow 0} (\epsilon + V^{\pi_{\epsilon}} (x)) \leq lim_{\epsilon \rightarrow 0} (\epsilon + sup_{\pi \in \prod} V^{\pi} (x)) = sup_{\pi \in \prod} V^{\pi} (x)\]

This shows that \(V^{*} = T^{*} V^{*}\) is upper bounded by the optimal value function within the space of stationary policies

Proof \(V^{*} (x) \geq sup_{\pi \in \prod} V^{\pi} (x)\)

Consider any \(\pi \in \prod\). By the definition of \(T^{\pi}\) and \(T^{*}\), for any \(V \in B(X)\), we have that for any \(x \in X\):

\[\begin{aligned} T^{\pi} V &= r^{\pi}(x) + \int P(dx^{\prime} | x, a) \pi(da | x) V(x^{\prime})\\ &= \int \pi(da | x) [P(dx^{\prime} | x, a) V(x^{\prime}) + r(x, a)]\\ &\leq sup_{a \in A} \{r(x, a) + \int P(dx^{\prime} | x, a) V(x^{\prime})\} = T^{*} V \end{aligned}\]

In particular, with the choice of \(V = V^{*}\), we have:

\[\begin{aligned} T^{\pi} V^{*} &\leq T^{*} V^{*} = V^{*}\\ \implies T^{\pi}T^{\pi} V^{*} &\leq T^{\pi}V^{*} \leq V^{*} \text{(Monotonicity)}\\ \implies (T^{\pi})^{k} V^{*} &\leq V^{*} \text{(apply bellman operator k times)} \end{aligned}\]

as \(k \rightarrow \infty\), by fix point theorem, we know that \((T^{\pi})^k V^{*} = V^{\pi}\):

\[\begin{aligned} \implies V^{\pi} &= lim_{k \rightarrow \infty} (T^{\pi})^k V^{*} \leq V^{*}, \forall \pi \in \prod\\ \implies V^{*} (x) &\geq sup_{\pi \in \prod} V^{\pi} (x) \end{aligned}\]

Thus, we can conclude that \(V^{*} (x) \geq sup_{\pi \in \prod} V^{\pi} (x)\)

Together, we showed that \(V^{*}\) is the same as \(V^{\pi^{*}}\), the solution of bellman optimality equation is the optimal value function