Dynamic Programming

We have defined concepts and properties such as value functions, bellman equations, bellman operators and etc. The question is how we can find the the optimal policy? Before we start, we assume that the dynamics of the MDP is given, that is, we know our transition distribution \(P\) and immediate reward distribution \(R\). The assumption of knowing the dynamics do not hold in the RL setting, but designing methods for finding the optimal policy with known model provides the foundation for developing methods for the RL setting.

DP methods benefit from the structure of the MDP such as the recursive structure encoded in the Bellman equation, in order to compute the value function.

Policy Evaluation

Policy Evaluation is the problem of computing the value function of a given policy \(\pi\) (i.e. find \(V^{\pi}\) or \(Q^{\pi}\)). This is not the ultimate goal of an RL agent (Finding the optimal policy is the goal), but is often needed as an intermediate step in finding the optimal policy

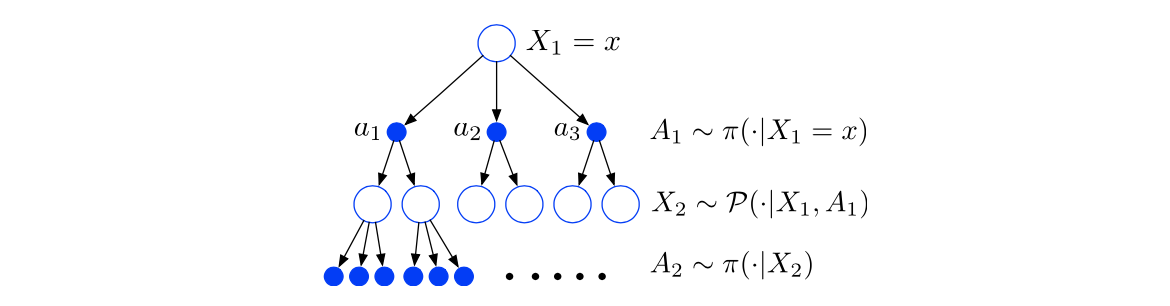
Given an MDP (\(X, A, P, R, \gamma\)) and a policy \(\pi\), we would like to compute \(V^{\pi}, Q^{\pi}\):

\[V^{\pi} (x) = E^{\pi}[\sum_{t=1}^{\infty} \gamma^{t-1} R_{t} | X_0 = x]\]

Control

Control is the problem of finding the optimal value function \(V^{*}, Q^{*}\) or \(\pi^{*}\)