Policy Iteration
Policy Iteration
A different approach is based on the iterative application of:
- Policy Evaluation: Given a policy \(\pi_k\), compute \(V^{\pi_k}, Q^{\pi_k}\)
- Policy Improvement: Find a new policy \(\pi_{k+1}\) that is better than \(\pi_{k}\), i.e., \(V^{\pi_{k+1}} \geq V^{\pi_k}\) (with a strict inequality in at least one state, unless at convergence)
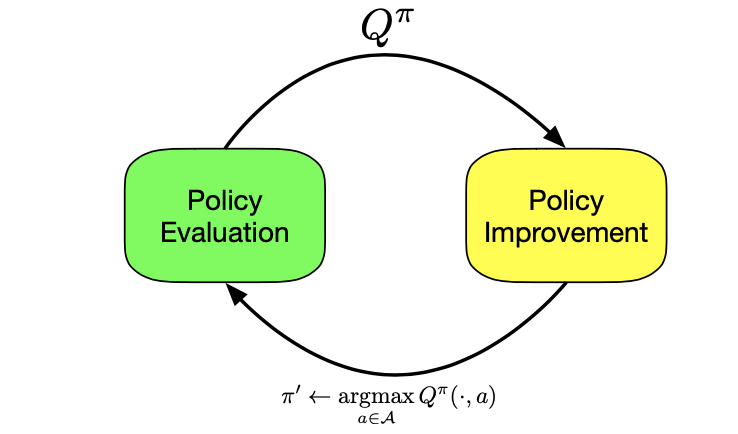
So, how do we perform policy evaluation and policy improvement?
Policy Evaluation: We can use the policy evaluation part of VI (\(V_{k+1} \leftarrow T^{\pi} V_{k}\)) to compute the value of a policy \(\pi_k\)
Policy Improvement: We take the greedy policy,
\[\pi_{k+1} \leftarrow \pi_g (x; Q^{\pi_k}) = argmax_{a \in A} Q^{\pi_k} (x, a), \forall x \in X\]
Why Greedy Policy? (Intuition)
Assume that at state \(x\), we act according to greedy policy \(\pi_g (x; Q^{\pi_{k}})\), and afterwards, we follow \(\pi_{k}\). (we modify our policy at state \(x\) to choose the greedy action)
The value of this new policy is:
\[Q^{\pi_k} (x, \pi_g (x; Q^{\pi_{k}})) = Q^{\pi_k} (x, argmax_{a \in A} Q^{\pi_k} (x, a)) = max_{a \in A} Q^{\pi_k} (x, a)\]
Compare \(max_{a \in A} Q^{\pi_k} (x, a)\) with \(V^{\pi_k} (x) = Q^{\pi_k} (x, \underbrace{\pi_k (x)}_{\text{any deterministic policy}})\), we can see that:
\[max_{a \in A} Q^{\pi_k} (x, a) = Q^{\pi_k} (x, \pi_g (x; Q^{\pi_{k}})) \geq Q^{\pi_k} (x, \underbrace{\pi_k (x)}_{\text{any deterministic policy}}) = V^{\pi_k} (x)\]
So this new policy is equal to or better than \(\pi_k\) at state \(x\).
Algorithm
Recall that:
\(V^{\pi_k}\) is an unique fixed point of bellman operator \(T^{\pi_{k}}\)
The greedy policy \(\pi_{k+1}\) satisfies:
\[\begin{aligned} T^{\pi_{k+1}} Q^{\pi_k} &= r(x, a) + \int P(dx^{\prime} | x, a) \underbrace{\pi_{k+1} (da^{\prime} | x^{\prime})}_{\text{This policy is greedy policy}} Q^{\pi_k} (x^{\prime}, a^{\prime})\\ &= r(x, a) + \int P(dx^{\prime} | x, a) Q^{\pi_k} (x^{\prime}, argmax_{a^{\prime} \in A} Q^{\pi_k} (x^{\prime}, a^{\prime})\\ &= r(x, a) + \int P(dx^{\prime} | x, a) max_{a^{\prime} \in A} Q^{\pi_k} (x^{\prime}, a^{\prime})\\ &= T^{*} Q^{\pi_{k}} \end{aligned}\]
We can summarize each iteration of the Policy iteration algorithm as:
(Policy Evaluation) Given \(\pi_k\), compute Q^{_k}, i.e find a Q that satisfies \(Q = T^{\pi_k} Q\)
(Policy Improvement) Obtain \(\pi_{k+1}\) as a policy that satisfies (select greedy policy at each state \(x\)):
\[T^{\pi_{k+1}} Q^{\pi_k} = T^{*} Q^{\pi_{k}}\]
We also have approximate policy iteration algorithms too, where policy evaluation or improvement steps (Truncate evaluation step, function approximation) are performed approximately:
\[Q \approx T^{\pi_k} Q\]
\[T^{\pi_{k+1}} Q^{\pi_k} \approx T^{*} Q^{\pi_{k}}\]
A generic algorithm can be found in Intro to RL book:

Implementation
Convergence of Policy Iteration
We can guarantee that the policy iteration algorithm converges to the optimal policy. For finite MDPs, the convergence happens in a finite number of iterations.
Policy Improvement Theorem

In other words, if we choose \(\pi^{\prime}\) to be the greedy policy, then we are guaranteed to have a better policy.
Poof
We have \(T^{*} Q^{\pi} \geq T^{\pi} Q^{\pi} = Q^{\pi}\) because for any \((x, a) \in X \times A\) it holds that:
Deterministic Policy \(\pi(x)\) \[r(x, a) + \gamma \int P(dx^{\prime} | x, a) max_{a^{\prime} \in A} Q^{\pi} (x^\prime, a^\prime) \geq r(x, a) + \gamma \int P(dx^{\prime} | x, a) Q^{\pi} (x^{\prime}, \pi(x^{\prime}))) \]
Stochastic Policy \(\pi(a | x)\)
\[r(x, a) + \gamma \int P(dx^{\prime} | x, a) max_{a^{\prime} \in A} Q^{\pi} (x^\prime, a^\prime) \geq r(x, a) + \gamma \int P(dx^{\prime} | x, a) \pi(da^{\prime} | x^{\prime}) Q^{\pi} (x^{\prime}, a^{\prime}))) \]
Thus, \[T^{\pi^{\prime}} Q^{\pi} = T^{*} Q^{\pi} \geq T^{\pi} Q^{\pi} = Q^{\pi}\]
We have:
\[T^{\pi^{\prime}} Q^{\pi} \geq Q^{\pi}\]
Then, we apply \(T^{\pi^\prime}\) to both sides, by monotonic property of bellman operator, we have:
\[T^{\pi^{\prime}}(T^{\pi^{\prime}} Q^{\pi}) \geq T^{\pi^{\prime}} Q^{\pi} = T^{*} Q^{\pi} \geq Q^{\pi}\]
Repeat this, we have for any \(m \geq 1\):
\[(T^{\pi^{\prime}})^{m} Q^{\pi} \geq T^{*} Q^{\pi} \geq Q^{\pi}\]
As \(m \rightarrow \infty\):
\[lim_{m \rightarrow \infty} (T^{\pi^{\prime}})^{m} Q^{\pi} = Q^{\pi^\prime}\]
\[\implies Q^{\pi^\prime} = lim_{m \rightarrow \infty} (T^{\pi^{\prime}})^{m} Q^{\pi} \geq Q^{\pi}\]