Value Iteration

Posted on Edited on In , Views:
Symbols count in article: 1.7k Reading time ≈ 2 mins.

Value Iteration

VI is one of the fundamental algorithms for planning. Many RL algorithms are essentially the sample-based variants of VI (DQN). We directly use the results of fixed points proposition and contraction property of the Bellman operator we proved in Bellman Optimality Equations.

Idea

Starting from \(V_0 \in B(X)\), we compute a sequence of \((V_{k})_{k \geq 0}\) by:

\[V_{k+1} \leftarrow T^{\pi} V_{k}\]

By the contraction property of the Bellman operator and Uniqueness of fixed points proposition :

\[lim_{k \rightarrow \infty} \| V_k - V^{\pi}\|_{\infty} = 0\]

similar for \(Q\):

\[lim_{k \rightarrow \infty} \| Q_k - Q^{\pi}\|_{\infty} = 0\]

Also, if we compute a sequence of \((V_{k})_{k \geq 0}\) by:

\[V_{k+1} \leftarrow T^{*} V_{k}\]

\[Q_{k+1} \leftarrow T^{*} Q_{k}\]

By the contraction property of the Bellman operator and Uniqueness of fixed points proposition, it is guaranteed that

\[lim_{k \rightarrow \infty} \| V_k - V^{*}\|_{\infty} = 0\]

\[lim_{k \rightarrow \infty} \| Q_k - Q^{*}\|_{\infty} = 0\]

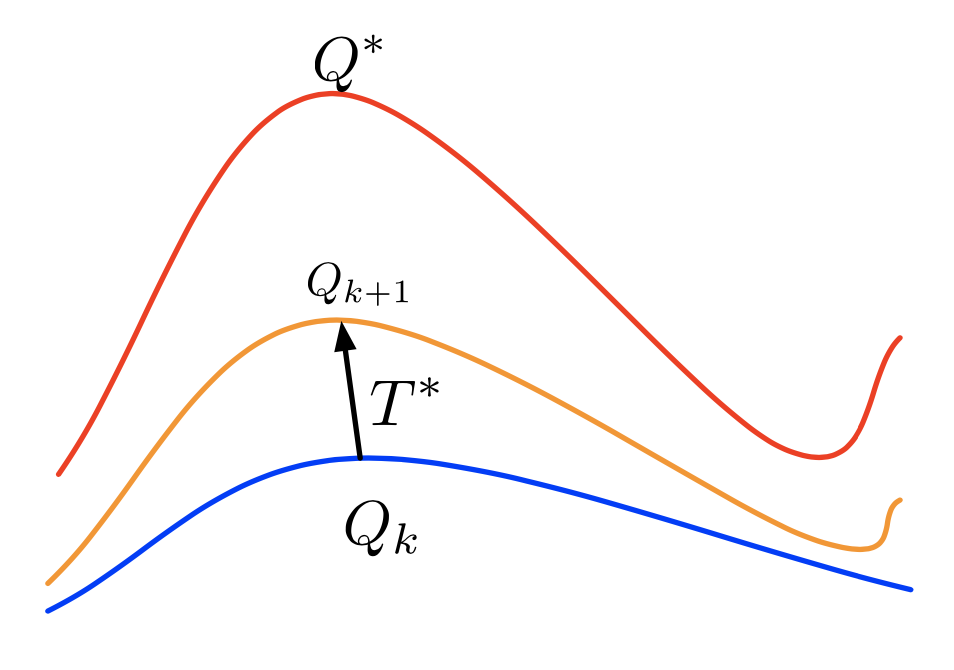
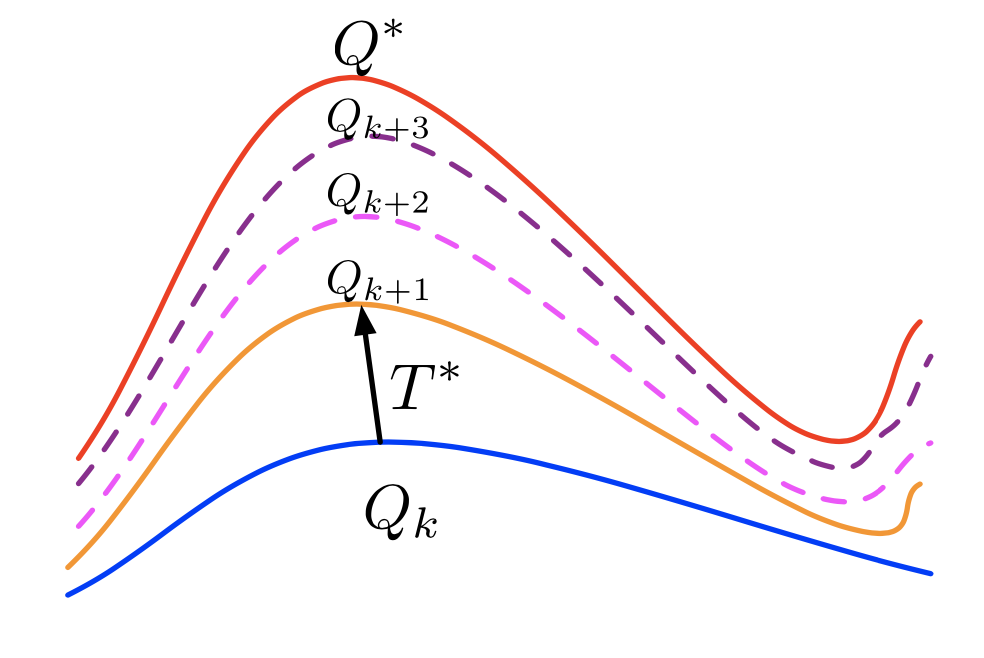
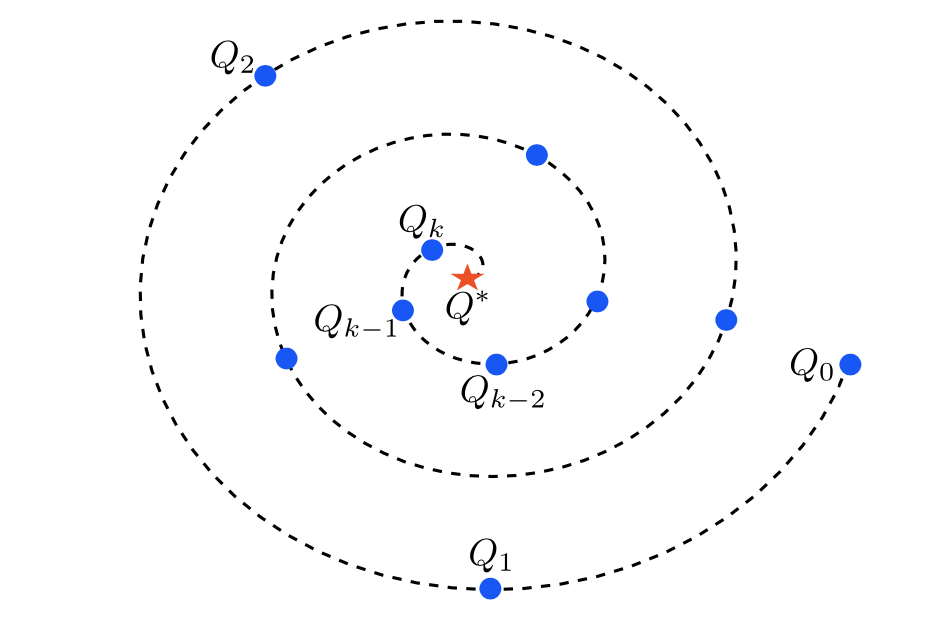
After finding \(Q^{*}\), finding optimal policy is straightforward:

\[\pi^{*} (a | x) = argmax_{a \in A} Q^{*} (x, a)\]

algorithm

One generic implementation can be found in intro to RL book:

Implementation

Below is one implementation of Value iteration (using Q):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# part of code from rl-algo.dp
# link: https://github.com/swag1ong/rl-algo

class ValueIter(DpBase):

    def train(self):

        dynamics = self.env.env.P

        while True:

            delta = 0
            # Calculate Q^*, V^* (s) = max_a Q^* (s, a)
            for s in dynamics.keys():
                prev_val = self._val[s].copy()
                curr_val = self._val[s]

                for a in dynamics[s].keys():
                    temp_val = 0

                    for p, s_prime, r, _ in dynamics[s][a]:
                        temp_val = temp_val + p * (r + self.gamma * np.max(self._val[s_prime]))

                    curr_val[a] = temp_val

                curr_delta = np.linalg.norm(np.array(prev_val) - np.array(curr_val))

                if curr_delta > delta:
                    delta = curr_delta

            if delta < self.threshold:
                break
Related Posts