DDQN

Deep Reinforcement Learning with Double Q-Learning

Introduction

The authors show that the double Q-learning algorithm which was first proposed in a tabular setting, can be generalized to arbitrary function approximation, including DNN. They use this to construct a new algorithm called double DQN to solve the overestimation problem in DQN.

Notations

Define:

\[Q_{\pi} (s, a) = E[R_1 + \gamma R_2 + ... | S_0=s, A_0=a, \pi]\]

\[Q_{*} (s, a) = max_{\pi} Q_{\pi} (s, a)\]

\[\pi_{*} (s) = argmax_{a \in A} Q_{*} (s, a)\]

The Target:

\[Y_t^{Q} = R_{t+1} + \gamma max_{a} Q(S_{t+1}, a; \theta_{t})\]

A standard Q update using stochastic gradient decent is (Semi-gradient Q):

\[\theta_{t+1} = \theta_t + \alpha (Y_{t}^{Q} - Q(S_t, A_t; \theta_t)) \nabla_{\theta_t} Q(S_t, A_t; \theta_t)\]

Where \(\alpha\) is a scalar step size.

Background

Double Q-learning

The max operator in standard Q-learning and DQN uses the same values both to select and to evaluate an action (ie. same Q is used to select the max action and use the value of this max action to update the Value of the state action pair). This makes it more likely to select overestimated values, resulting in overoptimistic value estimates.

In Double Q-learning, two value functions are learned by assigning experiences randomly to update one of the two value functions, resulting in two sets of weights, \(\theta\) and \(\theta^{\prime}\). For each update, one set of weights is used to determine the greedy action, and the other to determine its value.

Previous Q target:

\[Y_t^{Q} = R_{t+1} + \gamma Q(S_{t+1}, argmax_{a \in A} Q(S_{t+1}, a; \boldsymbol{\theta_t}); \boldsymbol{\theta_{t}})\]

The double Q-learning target:

\[Y_t^{\text{DoubleQ}} = R_{t+1} + \gamma Q(S_{t+1}, argmax_{a \in A} Q(S_{t+1}, a; \boldsymbol{\theta_t}); \boldsymbol{\theta^{\prime}_{t}})\]

Maximization Problem

This theorem shows that even if the value estimates are on average correct, estimation errors of any source can drive the estimates up and away from the true optimal values.

The lower bound in Theorem 1 decreases with the number of actions. This is an artifact of considering the lower bound, which requires very specific values to be attained. More typically, the overoptimism increases with the number of actions.

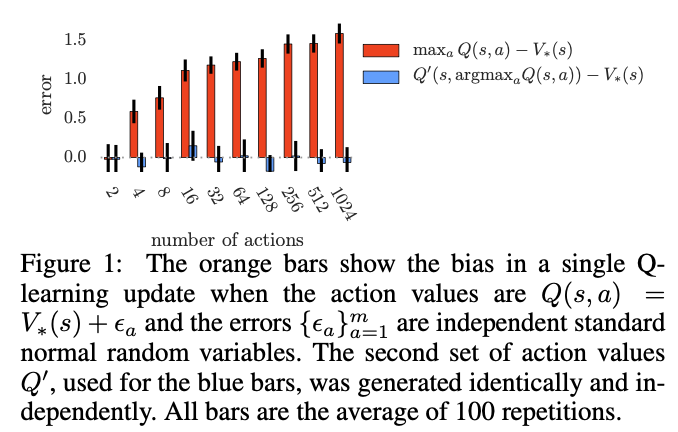
\[E[Q(s, a) - V_{*}(s)] = E[V_{*}(s) - V_{*}(s) + \epsilon ] = 0\]

But, Q-learning updates have large bias due to max operation, the phenomena is severer as number of actions increases.

In function approximation setting:

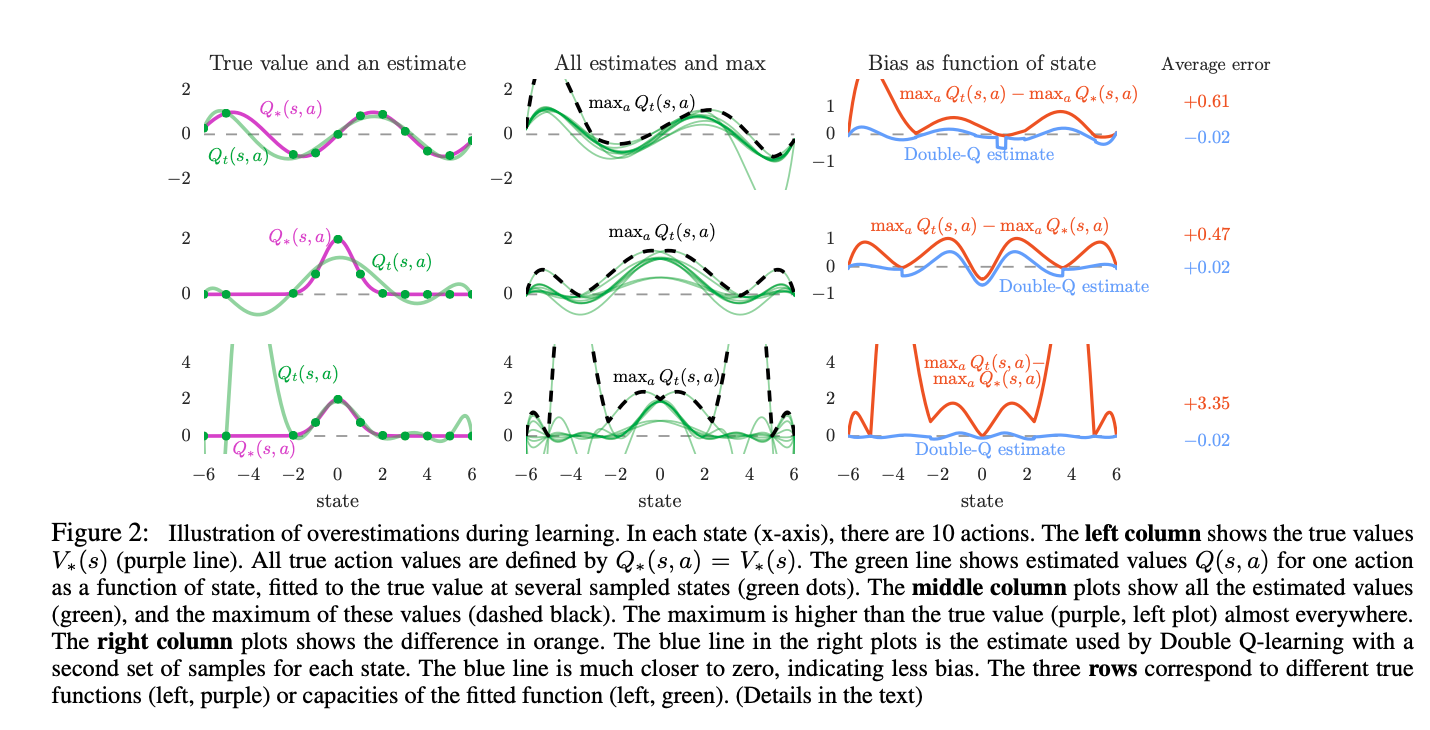
Algorithm

The target network in the DQN architecture provides a natural candidate for the second value function, without having to introduce additional networks. Thus, we can evaluate the greedy policy according to the online network, but using the target network to estimate its value. The resulting update:

\[Y_t^{\text{DoubleDQN}} = R_{t+1} + \gamma Q(S_{t+1}, argmax_{a} Q(S_{t+1}, a; \theta_{t}), \theta_{t}^{-})\]

Implementation

This is an implementation of DDQN in PARL. This implementation is written using PaddlePaddle.

https://github.com/PaddlePaddle/PARL

#   Copyright (c) 2020 PaddlePaddle Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
#     http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.

import copy
import parl
import paddle

class DQN(parl.Algorithm):
    
    def __init__(self, model, gamma=None, lr=None):
        """ DQN algorithm

        Args:
            model (parl.Model): forward neural network representing the Q function.
            gamma (float): discounted factor for `accumulative` reward computation
            lr (float): learning rate.
        """
        self.model = model
        self.target_model = copy.deepcopy(model)

        assert isinstance(gamma, float)
        assert isinstance(lr, float)
        self.gamma = gamma
        self.lr = lr

        self.mse_loss = paddle.nn.MSELoss(reduction='mean')
        self.optimizer = paddle.optimizer.Adam(
            learning_rate=lr, parameters=self.model.parameters())

    def predict(self, obs):
        """ use self.model (Q function) to predict the action values
        """
        return self.model.value(obs)

    def learn(self, obs, action, reward, next_obs, terminal):
        """ update the Q function (self.model) with DQN algorithm
        """
        # Q
        pred_values = self.model.value(obs)
        action_dim = pred_values.shape[-1]
        action = paddle.squeeze(action, axis=-1)
        action_onehot = paddle.nn.functional.one_hot(
            action, num_classes=action_dim)
        pred_value = paddle.multiply(pred_values, action_onehot)
        pred_value = paddle.sum(pred_value, axis=1, keepdim=True)

        # target Q
        with paddle.no_grad():
            greedy_actions = self.model.value(next_obs).argmax(1, keepdim=True)
            max_v = self.target_model.value(next_obs).gather(index=greedy_actions, axis=1)
            target = reward + (1 - terminal) * self.gamma * max_v

        loss = self.mse_loss(pred_value, target)

        # optimize
        self.optimizer.clear_grad()
        loss.backward()
        self.optimizer.step()
        return loss

    def sync_target(self):
        self.model.sync_weights_to(self.target_model)