Dropout
Dropout: A Simple Way to Prevent Neural Networks from Overfitting
The key idea of drop out is to randomly drop units along with their connections from the neural network during training to prevent overfitting. It can be interpreted as a way of regularizing a NN by adding noise to its hidden units.
Introduction
With unlimited computation, the best way to "regularize" a fixed-sized model is to average the predictions of all possible settings of the parameters, weighting each setting by the posterior probability given the training data (\(P(\theta | X)\)). This approach is not feasible in real life especially when there is large computational cost for training neural networks and training data are limited.Dropout prevents overfitting and provides a way of approximately combining exponentially many neural network architectures effectively.
Dropout temporarily removes units from the network along with all their incoming and outgoing connections. The choice of which units to drop is random.
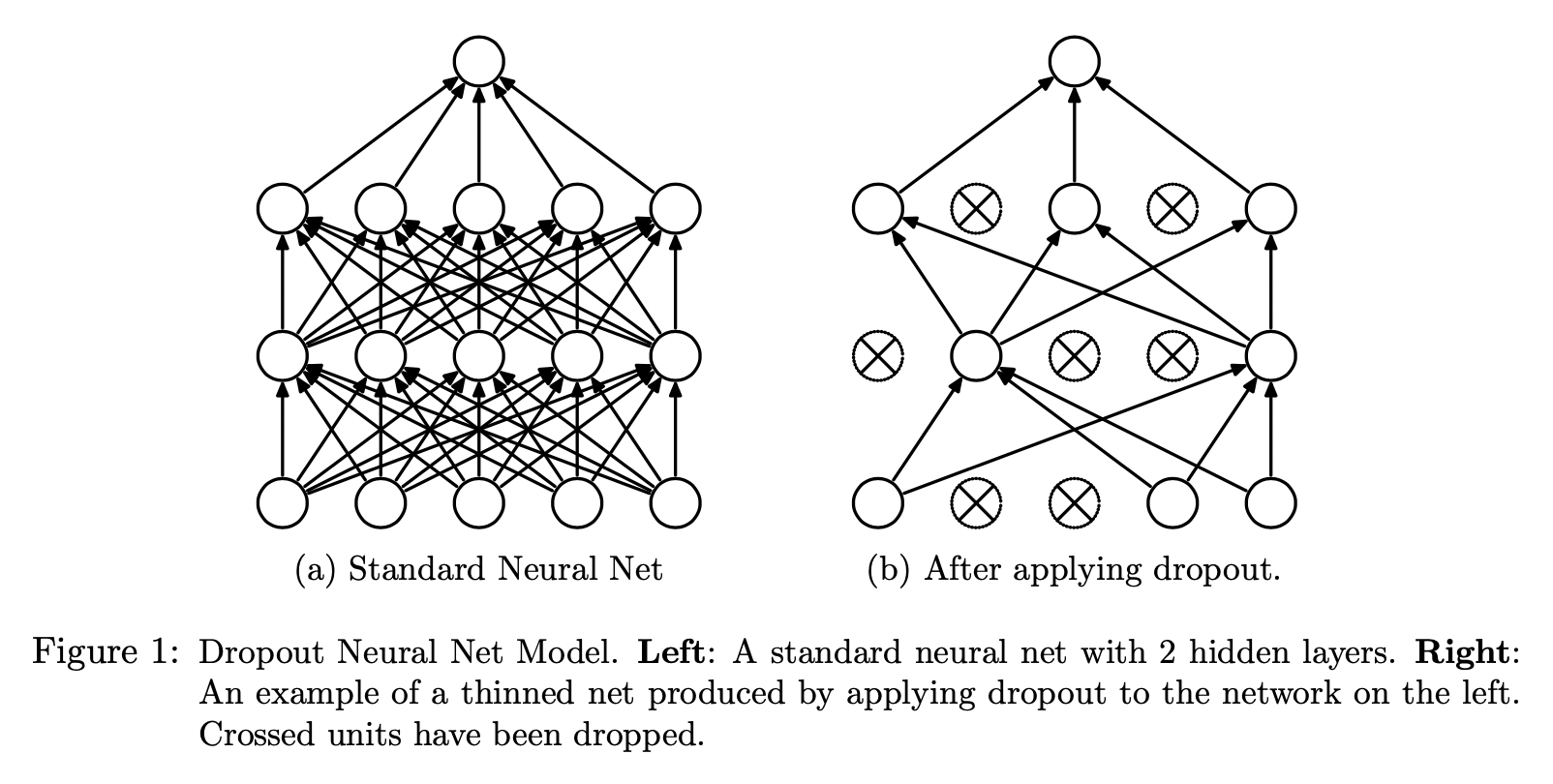
At training time, for a NN with \(n\) units, Dropout can be seen as training a collection of \(2^n\) (each unit can be retained or removed by dropout, so \(2^n\) different combinations) thinned networks (some units are dropped by dropout) with extensive weight sharing where each thinned network gets trained very rarely.
At test time, it is not feasible to explicitly average the predictions form exponentially many thinned models. However, we use a single NN without dropout by scaling-down the weights of this network. If an unit is retained with probability \(p\) during traning, the outgoing weights of that unit are multiplied by \(p\) at the test time. This ensures that the expected output is the same as the actual output at the test time (we use expected output at test time).
Model Description
Consider a NN with \(L\) hidden layers. Let \(l \in \{1, ..., L\}\) index the hidden layers of the network. Let \(\textbf{z}^{l}\) denote the vector of inputs into layer \(l\), \(\textbf{y}^{l}\) denote the vector of output from layer \(l\) (\(\textbf{y}^{0} = \textbf{x}\)). \(W^{l}\) and \(\textbf{b}^l\) are the weights and biases at layer \(l\). The standard forward operation can be described as:
\[z^{l + 1}_i = \textbf{w}_{i}^{l + 1} \textbf{y}^{l} + b_i^{l + 1}\]
\[y_i^{l+1} = f(z^{l + 1}_i)\]
Where \(W^l = [\textbf{w}_1^{l}, \textbf{w}_2^{l}, ...., \textbf{w}_{|l|}^{l}]\), \(f\) is any activation function.
With dropout, the forward operation becomes:
\[R_j^{l} \sim Bernoulli(p)\]
\[\tilde{\textbf{y}} = \textbf{R}^{l} * \textbf{y}^{l}\]
\[z^{l + 1}_i = \textbf{w}_{i}^{l + 1} \tilde{\textbf{y}}^{l} + b_i^{l + 1}\]
\[y_i^{l+1} = f(z^{l + 1}_i)\]
At the test time, the weights are scaled as \(W^{l}_{test} = p W^{l}\)
Backpropagation
Dropout NNs are trained using SGD in manner similar to standard NN. The only difference is that for each training case in the mini-batch, we sample a thinned network by dropping out units. Parameters that are dropped have zero gradients:
\[\tilde{\textbf{y}} = 0\]
\[\frac{\partial L}{\partial \textbf{w}_{i}^{l + 1}} = \frac{\partial L}{\partial z^{l + 1}_i} \frac{\partial z^{l + 1}_i}{\partial \textbf{w}_{i}^{l + 1}} = 0\]
One technique the authors found useful is to impose the max norm constraint on the weights during optimization such that:
\[\|w\|_{2} \leq c\]
Effect on Sparsity
The authors also found that as a side-effect of doing dropout, the activations of the hidden units become sparse, even when no sparsity inducing regularizes are present. Thus, dropout automatically leads to sparse representations.

Practical Guide for Training Dropout Networks
Network Size
It is to be expected that dropping units will reduce the capacity of a NN. At each training step (single training example or a mini-batch of examples), a subset of model parameters are optimized. Therefore, if \(n\)-sized layer is optimal for a standard NN on any given task, a good dropout net should have at least \(\frac{n}{p}\) units. This is a useful heuristic for setting the number of hidden units for convolutional and fully connected networks.
Learning Rate and Momentum
Dropout introduces a significant amount of noise in the gradients compared to standard SGD. Thus, a lot of gradients tend to cancel each other. In order ot make up for this, a dropout net should typically use 10-100 times the learning-rate that was optimal for a standard NN. Another way to reduce the effect of the noise is to use a high momentum. Using high learning rate and high momentum significantly speed up learning.
Max-norm Regularization
Though large momentum and learning rate speed up learning, they sometimes cause the weights to explode, so we need to apply some regularization on the parameter size.
Dropout Rate \(p\)
This hyperparameter controls the intensity of dropout. Small value of \(p\) requires big hidden unit size \(n\) which will slow down the training and leads to underfitting while large \(p\) may not produce enough dropout to prevent overfitting.