SVM

Support Vector Machine

Given dataset \(D = \{(\mathbf{x}_1, y_1) ....., (\mathbf{x}_N, y_N); \; \mathbf{x} \in \mathbb{R}^m, \; y_i \in \{-1, 1\}\}\). Let \(\mathbf{w}^T \mathbf{x} + b = 0\) be a hyperplane, we classify a new point \(\mathbf{x}_i\) by

\[ \hat{y}_i (\mathbf{x}_i) = \begin{cases} \mathbf{w}^T \mathbf{x}_i + b \geq 0, \quad \;\;\; 1\\ \mathbf{w}^T \mathbf{x}_i + b < 0, \quad -1\\ \end{cases} \]

Suppose that our data is linear separable. Then, \(\exists\) at least one possible combination of parameters \(\{\mathbf{w}, b\}\), such that:

\[\hat{\gamma}_i = y_i \hat{y}_i(\mathbf{x}_i) > 0, \; \forall i=1, ...., N\]

When \(y_i = 1\), a confident classifier would have \(\hat{y}_i(\mathbf{x}_i)\) as large as possible. On the other hand, when \(y_i = -1\), the confident classifier would have \(\hat{y}_i(\mathbf{x}_i)\) as negative as possible. Thus, we want \(\hat{\gamma}_i\) as large as possible, this \(\hat{\gamma}_i\) is called functional margin associated with training example for specific set of parameters \(\{\mathbf{w}, b\}\). And functional margin of \(\{\mathbf{w}, b\}\) is defined as minimum of these functions margins:

\[\hat{\gamma} = \min_{i=1, ..., N} \hat{\gamma}_i\]

In support vector machines the decision boundary is chosen to be the one for which the functional margin (confidence) is maximized.

Distance to Plane

Let \(\mathbf{x}_i\) be a sample that has label \(y_i = 1\), thus, it is on the positive side of the hyperplane \(\mathbf{w}^T \mathbf{x} + b = 0\). Define \(r\) to be the shortest distance between point \(\mathbf{x}_i\) and the hyperplane. Then \(r\) is the distance between \(\mathbf{x}_i\) to its projection on the hyperplane \(\mathbf{x}^{\prime}_i\).

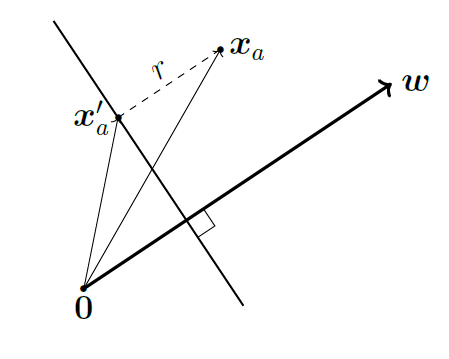
Since \(\mathbf{w}\) is the normal vector that is orthogonal to the plane and \(\frac{\mathbf{w}}{\|\mathbf{w}\|_2}\) is the unit vector that represents its direction. We can write the \(r\) as:

\[\mathbf{x}_i - \mathbf{x}^{\prime}_i = r \frac{\mathbf{w}}{\|\mathbf{w}\|_2}\]

\[\implies r = \frac{\mathbf{x}_i - \mathbf{x}^{\prime}_i}{\frac{\mathbf{w}}{\|\mathbf{w}\|_2}}\]

Goal

The concept of the margin is intuitively simple: it is the distance of the separating hyperplane to the closest examples in the dataset, assuming that our dataset is linearly separable. That is:

\[\begin{aligned} &\max \quad && \hat{\gamma}\\ &\;\text{s.t} \quad &&y_i (\mathbf{w}^T \mathbf{x}_i + b) \geq \hat{\gamma} \quad \quad \forall i=1, ...., N \end{aligned}\]

This optimization problem is unbounded, because one can make the functional margin large by simply scaling the parameters by a constant \(c\), \(\{c\mathbf{w}, cb\}\):

\[y_i (c\mathbf{w}^T \mathbf{x}_i + cb) > y_i (\mathbf{w}^T \mathbf{x}_i + b) = \hat{\gamma}\]

This has no effect on the decision plane because:

\[\mathbf{w}^T \mathbf{x}_i + b = c\mathbf{w}^T \mathbf{x}_i + cb = 0\]

Thus, we need to transform the optimization problem to maximize the distance between the samples and decision boundary instead of maximizing functional margin. Suppose we let all functional margins to be at least 1 (can easily achieve by multiplying parameters by a constant):

\[y_i (\mathbf{w}^T \mathbf{x}_i + b) \geq 1\]

\[\implies \mathbf{w}^T \mathbf{x}_i + b \geq 1\]

\[\implies \mathbf{w}^T \mathbf{x}_i + b \leq -1\]

Then, for point \(\mathbf{x}_i\) on \(\mathbf{w}^T \mathbf{x}_i + b = 1\), we have its distance to the decision plane:

\[\mathbf{w}^T \mathbf{x}_i + b - r \frac{\|\mathbf{w}\|^2_2}{\|\mathbf{w}\|_2} = 0\]

\[\implies r = \frac{1}{\|\mathbf{w}\|}\]

Then, we can formulate our objective as:

\[\begin{aligned} &\max_{\mathbf{w}, b} \quad && \frac{1}{\|\mathbf{w}\|_2}\\ &\;\text{s.t} \quad &&y_i (\mathbf{w}^T \mathbf{x}_i + b) \geq 1 \quad \quad \forall i=1, ...., N \end{aligned}\]

Which is equivalent to:

\[\begin{aligned} &\min_{\mathbf{w}, b} \quad && \frac{1}{2}\|\mathbf{w}\|^2_2\\ &\;\text{s.t} \quad &&y_i (\mathbf{w}^T \mathbf{x}_i + b) \geq 1 \quad \quad \forall i=1, ...., N \end{aligned}\]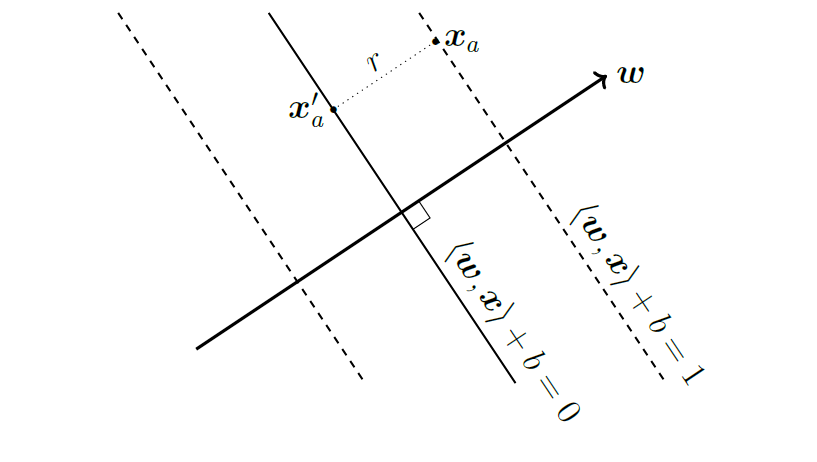

Soft Margin SVM

Slack Variables

Notice, in the above formulation, we have hard constraints on the margins which do not allow misclassification of points. However, in real world, data points are rarely linear separable and there will be outliers in the dataset, we may wish to allow some examples to be on the wrong side of the hyperplane or to have margin less than 1 .

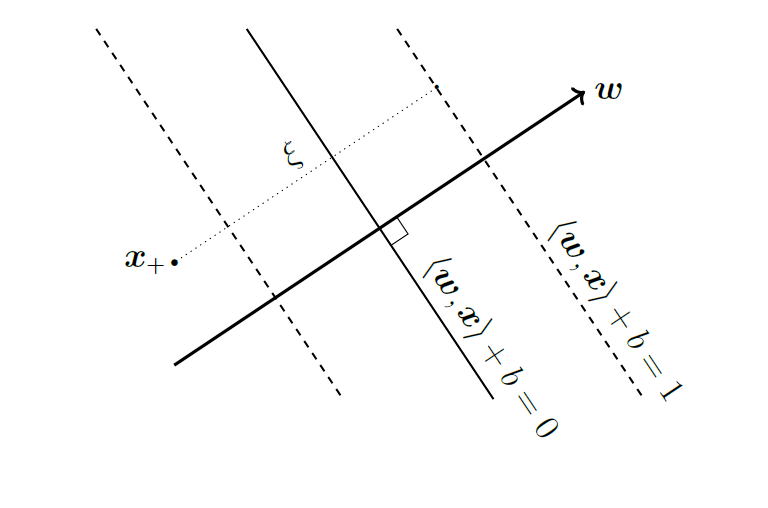
To resolve this problem, we can introduce slack variables one for each data point to relax the hard constraints:

\[y_i (\mathbf{w}^T \mathbf{x}_i + b) \geq 1 - \xi_i\] \[\quad\xi_i \geq 0, \; \; \forall i=1, ...., N\]

To encourage correct classification of the samples, we add \(\xi_i\) to the objective:

\[\begin{aligned} &\min_{\mathbf{w}, b, \boldsymbol{\xi}} \quad && \frac{1}{2}\|\mathbf{w}\|^2_2 + C\sum^{N}_{n=1} \xi_i\\ &\;\text{s.t} \quad &&y_i (\mathbf{w}^T \mathbf{x}_i + b) \geq 1 - \xi_i \quad &&&\forall i=1, ...., N\\ & && \xi_i \geq 0, &&&\forall i=1, ...., N \end{aligned}\]

Thus, sample points are now permitted to have margin less than 1, and if an example \(\mathbf{x}_i\) has slack variable greater than 0, we would have penalty in the objective function \(C\xi_i\). The parameter \(C\) controls the relative weighting between the twin goals of making the \(\|\mathbf{w}\|\) small and of ensuring that most examples have functional margin at least 1.

Dual Problem

Using Lagrange Multiplier, we can transform the constrained problem into an unconstrained concave problem:

\[\max_{\boldsymbol{\alpha}, \boldsymbol{\eta}}\;\min_{\mathbf{w}, b, \boldsymbol{\xi}} \; \frac{1}{2}\|\mathbf{w}\|^2_2 + C\sum^{N}_{n=1} \xi_i - \sum^N_{i=1} \alpha_i [y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i] - \sum^{N}_{i=1} \eta_i \xi_i\]

Where the inner minimization is the dual function and the maximization w.r.t \(\alpha\) is called dual problem.

KKT

For an unconstrained convex optimization problem, we know we are at global minimum if the gradient is zero. The KKT conditions are the equivalent conditions for the global minimum of a constrained convex optimization problem. \(\forall i=1, ...., N\):

1. Stationarity, If the strong duality holds, \((\mathbf{w}^*, \boldsymbol{\alpha}^*)\) is optimal, then \(\mathbf{w}^*\) minimizes \(L(\mathbf{w}^*, \boldsymbol{\alpha}^*)\) (same for \(b^*, \xi^*\) which are formulated as constraints in the dual problem):

   \[\nabla_{\mathbf{w}} L(\mathbf{w}^*, \boldsymbol{\alpha}^*) = 0\] \[\implies \mathbf{w}^* = \sum_{i=1}^{n} \alpha^*_i y_i \mathbf{x}_i\]

2. Complementary Slackness: \[\alpha_i [y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i] = 0\]

3. Primal Feasibility: \[y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i \geq 0\] \[\eta_i\xi_i = 0\]

4. Dual Feasibility: \[\alpha_i, \eta_i, \xi_i \geq 0\]

Solving Dual Problem

We now solve for the dual function by fixing \(\{\alpha_i\, \eta_i\}\) (satisfying Stationarity condition):

\[\min_{\mathbf{w}, b, \boldsymbol{\xi}} \frac{1}{2}\|\mathbf{w}\|^2_2 + C\sum^{N}_{n=1} \xi_i - \sum^N_{i=1} \alpha_i [y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i] - \sum^{N}_{i=1} \eta_i \xi_i\]

\[\begin{aligned} & \frac{\partial L(\mathbf{w}, b, \boldsymbol{\xi})}{\partial \mathbf{w}} = \mathbf{w} - \sum_{i=1}^{n} \alpha_i y_i \mathbf{x}_i = 0 \\ & \implies \mathbf{w}^* = \sum_{i=1}^{n} \alpha_i y_i \mathbf{x}_i \\ & \frac{\partial L(\mathbf{w},, b, \boldsymbol{\xi})}{\partial b} =\sum_{i=1}^{n} \alpha_i y_i = 0 \\ & \implies \sum_{i=1}^{n} \alpha_i y_i = 0 \\ & \frac{\partial L(\mathbf{w}, b, \boldsymbol{\xi})}{\partial \xi_n} = C - \alpha_n - \eta_n = 0 \\ & \implies \alpha_n = C - \eta_n \end{aligned}\]

Substitute back to the original equation, we obtain the dual function:

\[g(\boldsymbol{\alpha}) = -\frac{1}{2}\sum_{i=1}^{N}\sum_{k=1}^{N}\alpha_i \alpha_k {\mathbf{x}_i}^T \mathbf{x}_k y_i y_k + \sum_{i=1}^{N} \alpha_i\]

Then, we have the dual problem:

\[\begin{aligned} & \underset{\boldsymbol{\alpha}}{\text{max}} & & g(\boldsymbol{\alpha}) = -\frac{1}{2}\sum_{i=1}^{N}\sum_{k=1}^{N}\alpha_i \alpha_k {\mathbf{x}_i}^T \mathbf{x}_k y_i y_k + \sum_{i=1}^{N} \alpha_i\\ & \text{subject to} & & 0 \leq \alpha_i \leq C \\ & & & \sum_{i=1}^{n} \alpha_i y_i = 0 \\ \end{aligned}\]

This is a quadratic programming problem that we can solve using quadratic programming.

Interpretation

We could conclude:

1. if \(0 < \alpha_i < C \implies y_i(w^T x_i + b) = 1 - \xi_i\) Since \(\alpha_i = C - \mu_i, \mu_i \geq 0\), we have \(\xi_i =0 \implies\) the points are with \(0 < \alpha_i < C\) are on the margin

2. if \(\alpha_i = C\)

   • \(0 < \xi_i < 1\): the points are inside the margin on the correct side
   • \(\xi_i = 1\): the points are on the decision boundary
   • \(\xi_i > 1\): the points are inside the wrong side of the margin and misclassified

3. if \(\alpha_i = 0\), the points are not support vectors, have no affect on the weight.

After finding the optimal values for \(\boldsymbol{\alpha}\), we obtain optimal \(\mathbf{w}^*\) by solving:

\[\mathbf{w}^* = \sum_{i=1}^{n} \alpha^*_i y_i \mathbf{x}_i\]

We obtain optimal \(b^*\) by realizing that the points on the margins have \(0 < \alpha_i < C\). Let \(\mathbf{x}_i\) be one of those points, then:

\[{\mathbf{w^*}}^T \mathbf{x}_i + b = y_i\]

Let \(M\) be the set of all points that lies exactly on the margin, a more stable solution is obtained by averaging over all points:

\[b^* = \frac{1}{N_m} \sum^{N_m}_{i=1} (y_i - {\mathbf{w^*}}^T\mathbf{x}_i)\]

Kernel Tricks

Implementation

from cvxopt import matrix, solvers
import numpy as np
from qpsolvers import solve_qp
from sklearn.svm import SVC

class SVM:

    def __init__(self, c=1, kernel='linear'):
        self.c = c
        self.kernel = kernel
        self.b = None
        self.dual_coef_ = None
        self.decision_matrix = None

    def fit(self, X, y):
        n, d = X.shape
        y = y.reshape(-1, 1)
        yyt = np.matmul(y, y.T)
        P = np.zeros((n, n))
        q = matrix(-np.ones((n, 1)))
        a = matrix(y.T, tc='d')
        b = matrix([0.0])
        G = matrix(np.row_stack([np.diag([-1] * n), np.diag([1] * n)]), tc='d')
        h = matrix(np.row_stack([np.array([0] * n).reshape(n, 1),
                                 np.array([self.c] * n).reshape(n, 1)]), tc='d')
        for i in range(n):
            for j in range(n):
                P[i][j] = self.apply_kernel(X[i], X[j])

        P = matrix(P * yyt)
        alpha = np.array(solvers.qp(P, q, G, h , a, b)['x'])
        alpha[alpha < np.mean(alpha) * 0.1] = 0
        temp_x = np.column_stack([X, alpha, y])
        m = temp_x[(temp_x[:, -2] > 0) & (temp_x[:, -2] < self.c)]
        N_m = len(m)
        self.decision_matrix = m[:, :-2]
        self.b = 0
        self.dual_coef_ = m[:, -1] * m[:, -2]

        ## get b
        for i in range(N_m):
            self.b += m[i, -1]
            for j in range(N_m):
                self.b -= m[j, -2] * m[j, -1] * self.apply_kernel(m[i, :-2], m[j, :-2])

        self.b = self.b / N_m

        return self

    def apply_kernel(self, x_1, x_2):
        if self.kernel == 'linear':
            return np.dot(x_1, x_2)

    def decision_function(self, X):
        pred_results = np.array([])
        for i in range(len(X)):
            pred = self.b
            for j in range(len(self.decision_matrix)):
                pred += self.dual_coef_[j] * self.apply_kernel(X[i], self.decision_matrix[j])

            pred_results = np.append(pred_results, pred)

        return pred_results

    def predict(self, X):
        pred_results = self.decision_function(X)
        
        return np.where(pred_results >= 0, 1, -1)

Ref

https://www.ccs.neu.edu/home/vip/teach/MLcourse/6_SVM_kernels/lecture_notes/svm/svm.pdf

http://www.cs.cmu.edu/~guestrin/Class/10701-S06/Slides/svms-s06.pdf

MML book

Lagrangian Duality for Dummies, David Knowles

PRML Chapter 7