TCN

Temporal Convolutional Networks

Characteristics of TCN:

1. The convolutions in the architecture are causal.
2. The architecture can take a sequence of any length and map it to an output sequence of same length.
3. The ability of long term memories using a combination of very deep networks (with residual layers) and dilated convolutions.

Fully Convolutional Network

Fully convolutional networks replace the fully connected layers with convolution layers. The TCN uses a \(1D\) fully-convolutional network architecture, where each hidden layer is the same length as the input layer and zero padding of length (kernel - 1) in the front of the sequence is added to keep subsequent layers the same length as previous ones.

Causal Convolutions

To achieve the causality, the TCN uses causal convolutions, convolutions where an output at time \(t\) is convolved only with elements from time \(t\) and earlier in the previous layer. Thus:

\[\text{TCN} = 1D\text{FCN} + \text{causal convolutions}\]

The major disadvantage of this design is that we need an extremely deep network or very large filters to achieve a long effective history size.

Dilated Convolutions

The solution is to introduce dilated convolutions:

\[F_d(\mathbf{x}, s) = \sum^{k-1}_{i=0} f(i) \cdot \mathbf{x}_{s - d\cdot i}\]

Where \(f(i)\) is the \(i\)th component of the 1D filter with length \(k - 1, i=0, ...., k-1\) and \(d\) is the dilation factor, \(k\) is the filter size, and \(s - d \cdot i\) accounts for the direction of the past. Using large dilation enables an output at the top level to represent a wider range of inputs, thus effectively expanding the receptive field of a ConvNet. Thus, we can choose to: 1. Larger filter size \(k\). 2. Choose larger Dilation factor \(d\). Usually it is increased exponentially with the depth of the network \(d = 2^i\) at level \(i\) of the network. This ensures that there is some filter that hits each input within the effective history, while also allowing for an extremely large effective using deep networks.

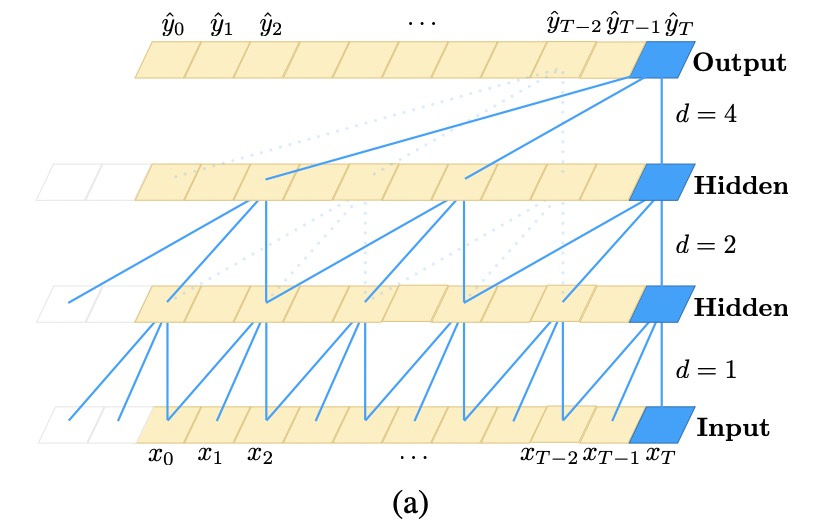
Residual Connections

To allow faster learning , a residual block is introduced with weight norm and dropout inbetween to replace the convolution layer:

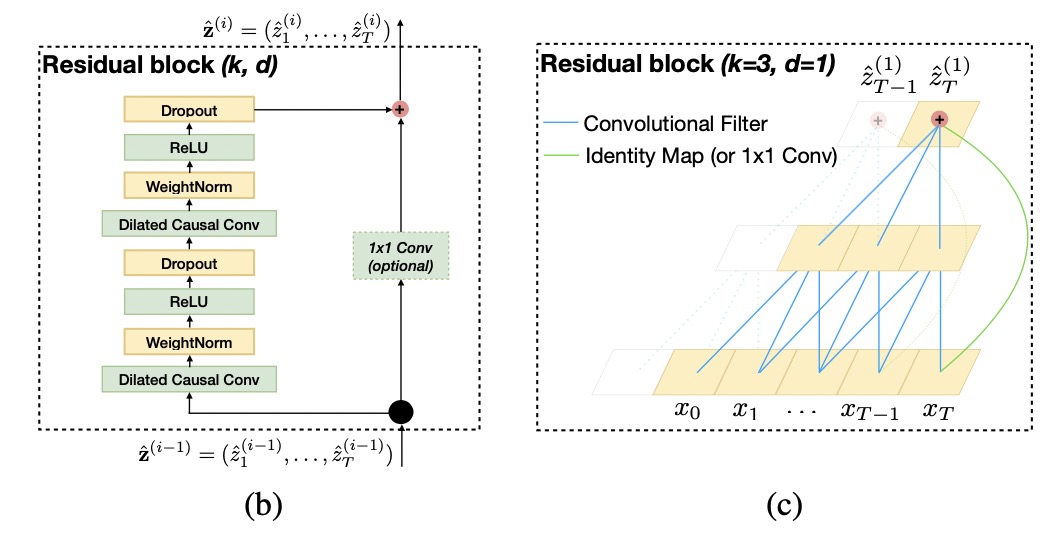
In TCN, the input and output of the residual block could have different widths (channels), to account for discrepant input-output widths, we use an additional \(1 \times 1\) convolution to ensure that elementwise addition will work.

Advantages of TCN

1. Parallelism:
2. Flexible Receptive Field Size
3. Stable Gradients
4. Low Memory Requirement for Training
5. Variable length inputs

Disadvantages of TCN

1. Data storage during evaluation:
2. Potential parameter change for a transfer of domain: