Dynamic Programming

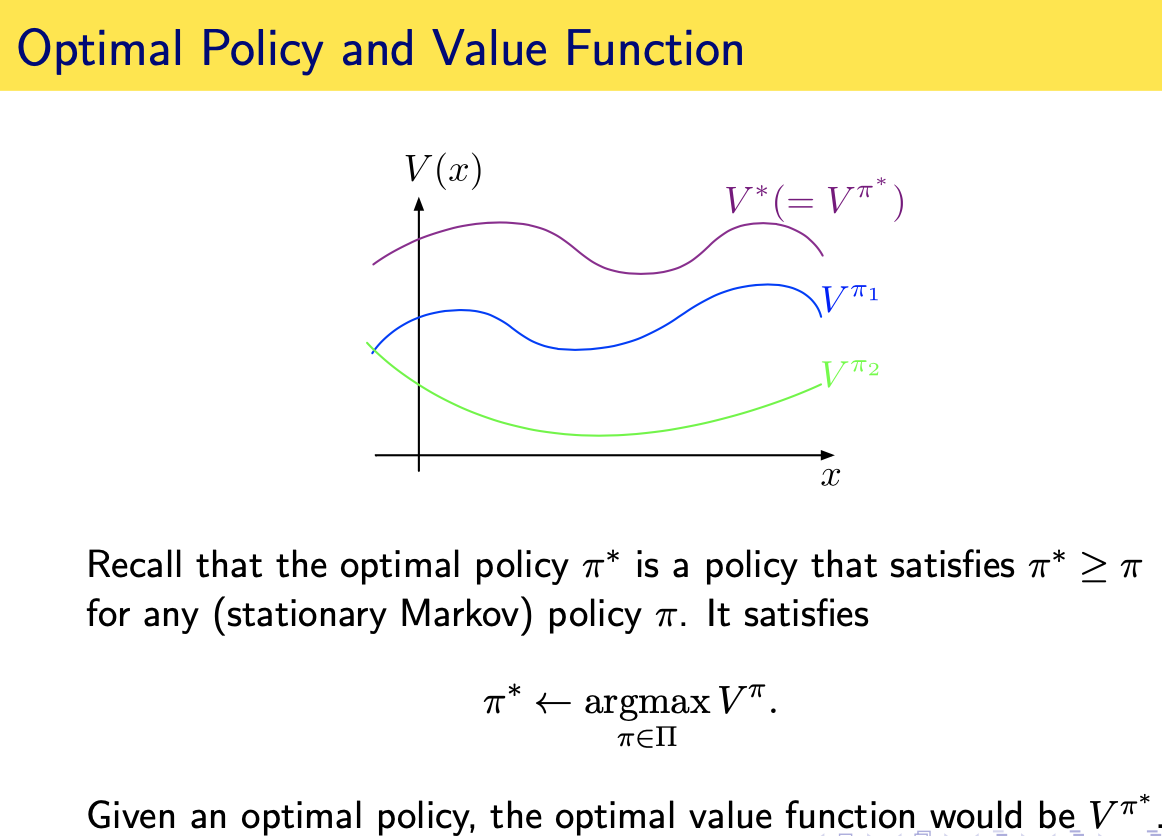
We have defined concepts and properties such as value functions, bellman equations, bellman operators and etc. The question is how we can find the the optimal policy? Before we start, we assume that the dynamics of the MDP is given, that is, we know our transition distribution \(P\) and immediate reward distribution \(R\). The assumption of knowing the dynamics do not hold in the RL setting, but designing methods for finding the optimal policy with known model provides the foundation for developing methods for the RL setting.

DP methods benefit from the structure of the MDP such as the recursive structure encoded in the Bellman equation, in order to compute the value function.

Please read posts on MDP and Bellman Equations prior this post.

Bellman Equations for Optimal Value Functions

So it is natural to ask, does the optimal value function of optimal policy \(V^{\pi^*}\) have similar recursive structure? the answer is yes, however, we need to prove this. The proof goes with 3 claims which we will prove later:

Please read post on MDP prior this post

Bellman Equations

By expanding value functions, we reveal the recursive property of return:

\[ \begin{aligned} V^{\pi} (x) &= E[G^{\pi}_{t} | X_{t} = x]\\ & = E[R_{t} + \gamma G^{\pi}_{t+1} | X_{t} = x]\\ & = E_{a \sim \pi(a | s)}[R_{t} | X_{t} = x] + \gamma E[G^{\pi}_{t+1} | X_{t} = x]\\ & = r^{\pi} (x) + \gamma E[V^{\pi} (X_{t+1}) | X_{t} = x]\\ \end{aligned} \]

MDP

Based on Prof Amir-massoud Farahmand's Lecture on RL

Define our MDP different from Introduction to RL book:

Where \(M(X)\) is the space of all probability distributions defined over the state space X